3 de março de 2021

O limite de resistência à tração é a tensão no ponto máximo da curva tensão-deformação. É a máxima tensão que pode ser sustentada por uma estrutura que se encontra sob tração.
A resistência à tração de um material é a quantidade máxima de tensão de tração que ele pode suportar antes da falha, por exemplo, quebra. Por isso, na indústria em geral, é necessário conhecer esse limite para diversos materiais.
Gráfico de tensão x deformação de material polimérico. Compósito com matriz poliéster e tecido de fibra de carbono. Ensaio realizado nas direções (45°,-45°). Material produzido por laminação manual.
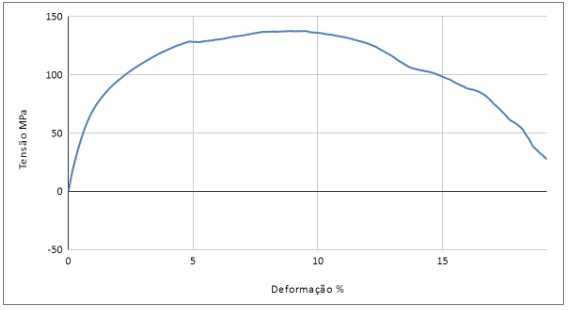
Fonte: [Autor]
Sumário
Limite de resistência à tração (UTS – do inglês: Ultimate tensile strength), muitas vezes reduzida para resistência à tração (TS – do inglês – tensile strength), é a resistência máxima ou Ftu, é a tensão máxima que um material pode suportar ao ser tracionado antes de quebrar. Em materiais frágeis, a resistência à tração final está perto do ponto de escoamento, enquanto que em materiais dúcteis a resistência à tração final pode ser maior [1].
A resistência à tração final geralmente é encontrada realizando um teste de tração e registrando a tensão de engenharia versus deformação. O ponto mais alto da curva tensão-deformação é a resistência à tração final e tem unidades de tensão (MPa) [1].
O limite de resistência à tração raramente é usado no projeto de materiais dúcteis, mas são importantes em materiais frágeis, uma vez que em materiais dúcteis, normalmente se usa o limite de escoamento para a escolha do material. Eles são tabulados para materiais comuns, como ligas, materiais compósitos, cerâmicas, plásticos e madeira [1].
Esta característica de um material é uma propriedade intensiva; portanto, seu valor não depende do tamanho do corpo de prova. No entanto, dependendo do material, pode ser dependente de outros fatores, como a preparação da amostra, a presença ou não de defeitos de superfície e a temperatura do ambiente de teste e do material [1].
Alguns materiais quebram muito bruscamente (frágeis), sem deformação plástica, o que é chamado de falha frágil. Outros, que são mais dúcteis, incluindo a maioria dos metais, experimentam alguma deformação plástica e possivelmente estrangulamento antes da fratura [1].
A resistência à tração é definida como uma tensão, que é medida como força por unidade de área. Para alguns materiais não homogêneos (ou para componentes montados), pode ser relatado apenas como uma força ou como uma força por unidade de largura.
No Sistema Internacional de Unidades (SI), a unidade é o pascal (Pa) (ou um múltiplo dele, geralmente megapascals (MPa), usando o prefixo SI mega); ou, equivalentemente a pascais, newtons por metro quadrado (N / m²) [1].
Aqui não iremos tratar do impacto da temperatura nas propriedades mecânicas dos materiais. Mas de maneira geral, é possível que os materiais, principalmente em polímeros e metais, fiquem mais frágeis.
Materiais cerâmicos apresentam uma característica muito singular quanto ao gráfico de tensão de formação. Ele se comporta como uma reta, e por não terem, normalmente, um regime plástico, o limite de escoamento, apresentado em outros gráficos como os de polímeros ou metais, é na verdade o limite de ruptura, ou mesmo o limite de resistência à tração do material [1]. A Figura 1 apresenta um gráfico de alumina e de um vidro.
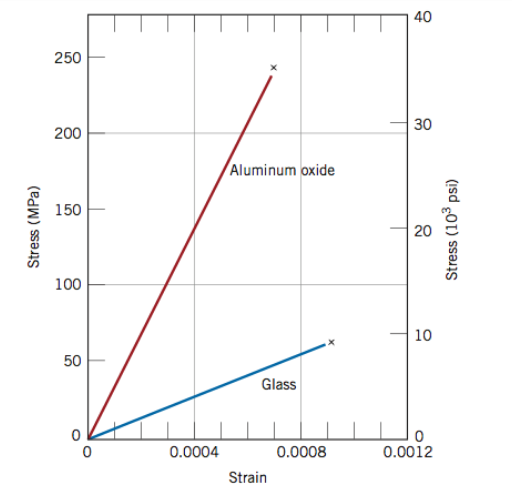
Fig. 1 – Curvas de tensão-deformação para dois materiais frágeis [1].
Uma das áreas da engenharia mais importantes no Brasil é a construção civil. Onde, o concreto, um material cerâmico / compósito se apresenta mais evidente nas construções.
A resistência à tração é importante quando se considera trincas em elementos do concreto. Os fatores que influenciam a resistência à compressão também influenciam a resistência à tração. As principais diferenças entre o concreto agregado leve e o concreto normal são devido ao percurso da trinca durante sua propagação [2].
Normalmente as trincas se propagam através das partículas de agregados leves, ao invés de ao redor delas. O comportamento é semelhante ao concreto feito com agregados triturados em que a relação resistência à flexão / compressão é maior [2]. Tais trincas podem ser geradas devido a tração aplicada ou mesmo por ter elementos que podem influenciar nesse processo de quebra.
Defeitos na rede, em geral, podem diminuir a resistência mecânica dos materiais. O efeito de pequenas falhas críticas na resistência de materiais cerâmicos policristalinos deve ser analisado com a ajuda de um critério de iniciação combinando condições de tensão e energia [3].
Se o tamanho do defeito for menor do que o comprimento característico do material, as previsões numéricas revelam que o defeito (pontiagudo ou rombudo) não tem efeito sobre a resistência. Este resultado está de acordo com os resultados experimentais obtidos nas medidas de resistência de materiais cerâmicos com defeitos controlados. Testes de fratura após a introdução de falhas com tamanhos controlados permitem identificar os parâmetros de fratura do material cerâmico [3].
Uma questão fundamental que afeta a funcionalidade, vida útil e confiabilidade mecânica de tais componentes e sistemas é a iniciação e propagação descontrolada de rachaduras nas peças cerâmicas quebradiças. Ao contrário dos metais ou polímeros, a propagação de fissuras em cerâmica é geralmente catastrófica devido à falta de deformação plástica durante o carregamento de tração [3, 4].
Diz-se que as cerâmicas têm baixa tolerância ao dano, devido à sua baixa resistência à propagação de trincas (baixa tenacidade à fratura). Outra limitação para aplicações que exigem alta confiabilidade é a dispersão inerente na resistência causada pelo diferente tamanho, tipo e localização de falhas críticas na cerâmica (por exemplo, poros, não homogeneidade, defeitos de superfície, trincas de contato), introduzidas durante o processamento, usinagem ou em serviço [3, 4].
Como resultado dessa fragilidade, as peças de cerâmica possuem uma probabilidade inerente de falha, sua resistência sendo caracterizada por uma função de distribuição descrita na maioria dos casos pela teoria de Weibull [3, 4]
A resistência à tração das cerâmicas é muito sensível à presença de falhas, que geralmente atuam nucleando trincas [3, 5]. Falhas críticas comuns são poros esféricos gerados durante o processamento da cerâmica [3].
A relação entre tais falhas extrínsecas e a resistência da cerâmica é geralmente avaliada estimando-se um “comprimento de trinca equivalente” na ruptura [6], também denominado comprimento de trinca de Griffith, que é a base de uma análise mecânica da fratura elástica linear, e o balanço energético [3].
Por exemplo, no caso de um defeito como um poro arredondado, o comprimento de trinca equivalente é dado como uma pequena fissura radial na vizinhança do poro [6, 7]. No caso de um defeito agudo como um entalhe, assume-se que uma matriz de microfissuras ao longo da cunha do entalhe se desenvolve durante o carregamento, desencadeando assim a fratura do material quebradiço [3].
Por outro lado, não podemos usar um teste de tração para determinar a resistência da cerâmica, porque é difícil preparar as amostras com precisão. As amostras muitas vezes quebram nas garras e a cerâmica quebra após 0,1% de tensão, o que significa que a amostra deve estar perfeitamente alinhada para evitar qualquer flexão de tensões.
Falhas e compressão Normalmente, a resistência da cerâmica é testada usando um teste de flexão de quatro pontos.
Cerâmica tem resistência à compressão cerca de dez vezes maior do que sua resistência à tração. O limite de resistência à tração de cerâmicas e vidros é baixa porque as falhas existentes (tricas internas ou superficiais) atuam como concentradores de tensão. Isso ocorre porque as falhas não se propagam sob compressão. Como resultado disso, as cerâmicas são geralmente usadas em aplicações onde as cargas são compressivas.
À temperatura ambiente, tanto as cerâmicas quanto os vidros apresentam um comportamento onde ocorre a fratura rápida em um teste de tração antes que qualquer deformação plástica ocorra [1]. A cerâmica tem uma resistência à fratura cerca de cinquenta vezes menor do que os metais, embora suas forças de ligação sejam altas. A resistência à fratura de um material que falha por fratura rápida é dada por:
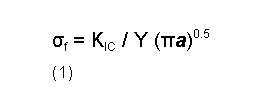
onde σf é a tensão aplicada, KIc é a tenacidade à fratura de deformação plana, Y é uma constante adimensional e a é o comprimento da trinca superficial ou metade do comprimento da trinca interna. Pode-se observar que a resistência à tração de uma cerâmica é determinada pelo comprimento da falha mais longa [1].
Os polímeros apresentam propriedades mecânicas interessantes. Enquanto as cerâmicas apresentam um limite de resistência à tração praticamente no mesmo ponto que o limite de ruptura, a maioria dos polímeros já apresentam um regime plástico. Por outro lado, para polímeros convencionais, sua dureza é bem menor que a das cerâmicas [1, 8].
Assim como nas cerâmicas, podemos considerar a fratura frágil utilizando a teoria de Griffith. A capacidade de propagação de trinca no material pode ser avaliada com a seguinte equação da tensão crítica (σc) que gera a propagação da trinca [8] :
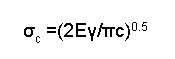
onde E é o módulo de elasticidade, γ é a energia superficial específica e c é o comprimento da trinca [8]. Após a tensão crítica, o material apresenta a ruptura.
Observando a equação 2, verifica-se que quanto maior o tamanho da trinca (c), menor será a tensão aplicada para apresentar a ruptura [8]. Uma das grandes implicações para o comportamento frágil dos polímeros é sua TG (temperatura de transição vítrea), que depende diretamente da temperatura do ambiente [8, 9, 10].
Considerando a TG dos polímeros, e a sua TM (temperatura de fusão), temos de maneira geral, comportamentos similares dos polímeros, como apresentado na Tabela 1:

Tabela 1 – Relação da cristalinidade, temperatura e comportamento mecânico [8, 9, 10].
A Figura 2 apresenta diferentes comportamentos para diferentes tipos de polímeros, inserindo a ideia de que, mesmo sendo polímero, o material pode apresentar um comportamento tão frágil como o de uma cerâmica.
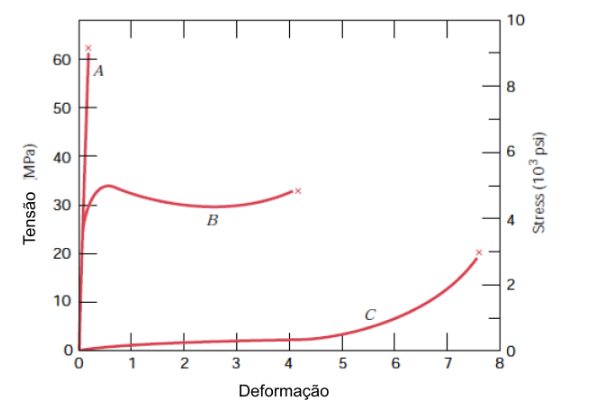
Fig. 2 – O comportamento tensão-deformação para polímeros frágeis (curva A), plásticos (curva B) e altamente elásticos (elastoméricos) (curva C) [1].
Materiais poliméricos apresentam estruturas muito interessantes, e que podem mudar dependendo de como o material é fabricado. Por exemplo, PVC é um material rígido, com limite de resistência à tração de aproximadamente 50.3 MPa [11] aproximadamente, enquanto o uso de um plastificante, tornando-o flexível, pode alterar este valor para 25 MPa [12].
Além do uso de plastificantes, materiais poliméricos podem apresentar diferentes valores para algumas propriedades mecânicas de acordo com a taxa de resfriamento. Taxas de resfriamento baixas podem tornar o material duro e frágil, pois o crescimento dos esferulitos é muito alto. Já para taxas de resfriamento altas, existe um menor crescimento dos esferulitos [8].
A Figura 3 apresenta uma representação de esferulito.
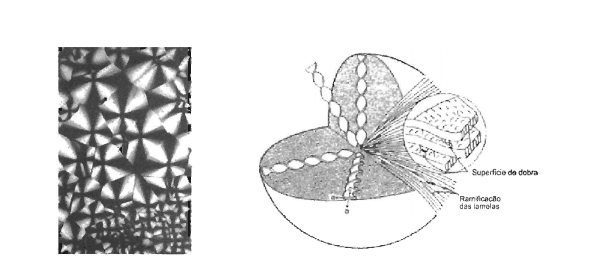
Fig. 3 – Micrografia óptica (mostrando a Cruz de Malta) e modelo de um esferulito. No detalhe têm-se lamelas cristalinas com fase amorfa (não mostrada) entre elas [8].
Lembrando que os esferulitos são as partes não amorfas da estrutura do material semicristalino.
Com isso, temos que nos atentar com o tipo de molde escolhido para a fabricação de peças poliméricas. Moldes fabricados com aço Toolox 33 apresentam um melhor produto final, pois sua taxa de resfriamento mais alta, além de produzir muito mais no mesmo tempo que o aço AISI P20, gera um polímero mais resistente e com boas propriedades mecânicas.
Está gostando do nosso conteúdo? Junte-se à nossa comunidade, inscreva-se na nossa Newsletter e receba conteúdos como esse diretamente no seu e-mail. ⬇

Durante o ensaio de tração, os metais apresentam uma curva bem característica, com vários pontos que nos mostram algumas propriedades. Normalmente, metais como aço ou alumínio por exemplo, apresentam algumas regiões destes gráficos, como uma região elástica, onde o material deforma pouco, mas volta ao seu estado original quando a força para de ser aplicada. A Figura 4 apresenta um gráfico genérico de tensão X deformação.
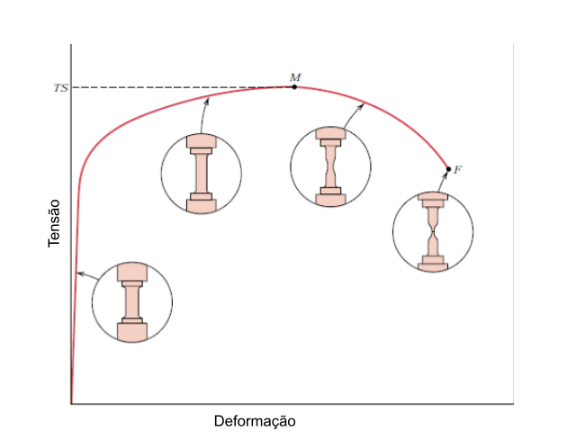
Figura 4 – Gráfico típico de tensão-deformação até a fratura, no ponto F. O limite de resistência à tração TS é indicada no ponto M. As inserções circulares representam a geometria da amostra dúcteis deformada em vários pontos ao longo da curva [1].
Existe outra região no gráfico que é o regime plástico, onde ocorre o encruamento do material pela deformação plástica. Neste caso, a deformação é permanente, e o material fica mais resistente à força aplicada. Logo, deve-se aplicar mais força para que ele deforme, até o limite de resistência à tração.
O limite de resistência à tração pode variar de 50 MPa para um alumínio a até 3000 MPa para os aços de alta resistência. Normalmente, quando a resistência de um metal é citada para fins de projeto, o limite de escoamento é usado [1], uma vez que a peça não pode deformar-se plasticamente.
Isso ocorre porque, no momento em que uma tensão correspondente à resistência à tração é aplicada, muitas vezes uma estrutura já passou por tanta deformação plástica que se torna inútil. Além disso, as resistências à fratura não são normalmente especificadas para fins de projeto de engenharia [1].
Por outro lado, existem técnicas de encruamento de aços, e outros metais, que envolvem a deformação plástica do material, gerando um refino de grão e aumento da dureza [13, 14, 15].
É interessante avaliar que, após a retirada da carga durante o teste de tensão-deformação, alguma fração da deformação total é recuperada como deformação elástica, como apresentado na Figura 5.
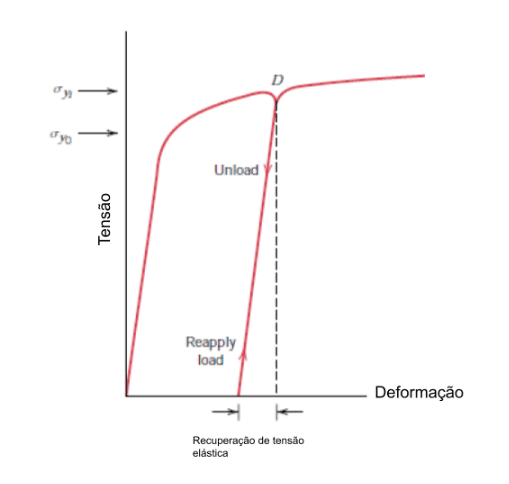
Figura 5 – Diagrama esquemático tensão-deformação de tração que mostra os fenômenos de recuperação de deformação elástica e endurecimento por deformação. σy0 é a resistência ao escoamento e σyi é a resistência ao escoamento após a liberação da carga no ponto D e, a seguir, na recarga [1].
Durante o ciclo de descarga, a curva traça um caminho quase em linha reta a partir do ponto de descarga (ponto D), e sua inclinação é virtualmente idêntica ao módulo de elasticidade, ou paralela à porção elástica inicial da curva. A magnitude dessa deformação elástica, que é recuperada durante a descarga, corresponde à recuperação da deformação.
Se a carga for reaplicada, a curva percorrerá essencialmente a mesma porção linear na direção oposta à descarga; o escoamento ocorrerá novamente no nível de estresse de descarregamento onde o descarregamento começou. Haverá também uma recuperação de tensão elástica associada à fratura.
Uma das vantagens dos materiais metálicos sobre as cerâmicas é que, os materiais cerâmicos são um tanto limitados em aplicabilidade por suas propriedades mecânicas, que em muitos aspectos são inferiores às dos metais. A principal desvantagem é a disposição para uma fratura catastrófica de uma maneira frágil com muito pouca absorção de energia. Nesta seção, exploramos as características mecânicas salientes desses materiais e como essas propriedades são medidas [1].
Por outro lado, temos aplicações onde tanto os aços, como cerâmicas podem ser aplicados juntos ou separados na mesma aplicação. Para fabricação de peças cerâmicas, como tijolos, é utilizado o aço AISI D6, mas junto com ele, insertos cerâmicos devem ser utilizados, por suas propriedades de não desgastar.
Já para ferramentas de usinagem, pode-se utilizar o aço rápido AISI M2, mas também algumas cerâmicas especiais.
Normalmente, o teste de tração envolve tirar uma pequena amostra com uma área transversal fixa e, em seguida, puxá-la com um tensiômetro a uma taxa de deformação constante (mudança no comprimento padrão dividido pelo comprimento padrão inicial) até que a amostra se rompa.
Ao testar alguns metais, a dureza de indentação se correlaciona linearmente com a resistência à tração. Essa relação importante permite testes não destrutivos economicamente importantes de entregas da matéria prima antes da usinagem, com equipamentos leves e até portáteis, como os testes de dureza Rockwell portáteis, ou durômetro portátil. Essa correlação prática ajuda a garantia de qualidade nas indústrias metalúrgicas a se estender muito além do laboratório e das máquinas de teste universais.
O teste de tração é um destrutivo que fornece informações sobre a resistência à tração, resistência ao escoamento e ductilidade do material. Ele mede a força necessária para quebrar uma amostra e a extensão na qual a amostra se estende ou se alonga (empescoçamento) até esse ponto de quebra [16].
O teste de tração de compósitos é geralmente na forma de tensão básica ou teste de tensão de sanduíche plano de acordo com padrões como ISO 527-4, ISO 527-5, ASTM D 638, ASTM D 3039 e ASTM C 297. Esses testes produzem gráficos de tensão-deformação usados para determinar o módulo de tração [16].
Como o ensaio se baseia em aplicar uma tensão na peça, gerando uma deformação plástica, no final do escoamento, a inclinação da curva aumenta novamente, o que mostra que o material pode sustentar uma carga adicional. Este fenômeno é chamado de encruamento [17], onde a peça apresenta maior resistência mecânica (dureza) devido ao movimento e geração de defeitos na rede. Muitos materiais metálicos podem passar por processo semelhante para apresentarem menor desgaste durante o trabalho [1, 17].
Enquanto a área da seção transversal diminui uniformemente ao longo de todo o comprimento da barra no caso de pequenas tensões, ela começa a diminuir localmente em tensões muito altas. Uma vez que a seção transversal real pode então ser consideravelmente menor que a seção transversal A original, a tensão σ = F / A não descreve mais a tensão real [17].
Portanto, é apropriado introduzir a tensão σt = F / Aa, que é chamado de tensão verdadeira ou tensão física. Representa a tensão verdadeira na região onde ocorre o empescoçamento. A tensão σ = F / A é referida como tensão nominal, convencional ou de engenharia. A Figura 6 apresenta ambas as tensões até que ocorra a fratura.
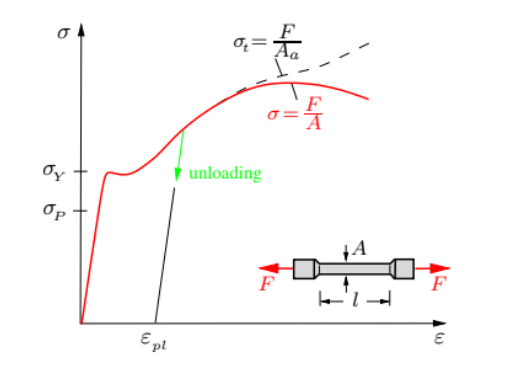
Fig. 6 – gráfico de tensão-deformação, mostrando as equações de tensão verdadeira e de engenharia.
O procedimento do teste é realizado da seguinte maneira. Uma amostra é colocada em uma máquina de ensaio universal. Normalmente, a seção transversal é circular, mas amostras retangulares também são usadas. Durante o teste, a deformação é confinada à estreita região central, que tem uma seção transversal uniforme ao longo de seu comprimento. O diâmetro padrão é de aproximadamente 12,8 mm [1],
Enquanto o comprimento da seção reduzida deve ser de pelo menos quatro vezes esse diâmetro; 60 mm. O comprimento de medida é usado em cálculos de ductilidade, o valor padrão é 50 mm. A amostra é montada pelas suas extremidades nas garras de retenção do aparelho de teste [1].
A máquina de teste de tração é projetada para alongar o corpo de prova a uma taxa constante e para medir contínua e simultaneamente a carga aplicada instantânea (com uma célula de carga) e os alongamentos resultantes (usando um extensômetro). Um teste de tensão-deformação normalmente leva vários minutos para ser executado e é destrutivo; ou seja, o corpo de prova está permanentemente deformado e geralmente fraturado [1]. A Figura 7 apresenta um esquema de como é realizado o teste.
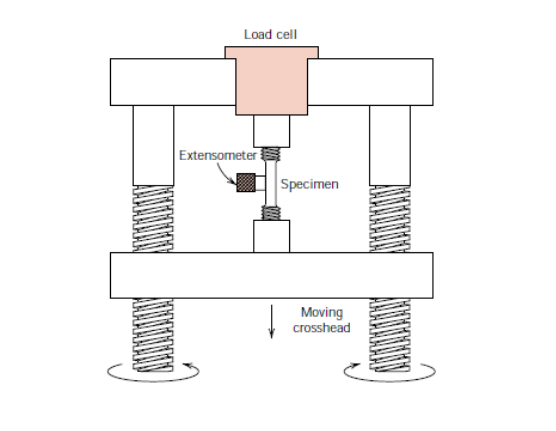
Fig. 7 – Representação esquemática do aparelho usado para realizar testes de tensão-deformação de tração. A amostra é alongada pela cruzeta móvel; a célula de carga e o extensômetro medem, respectivamente, a magnitude da carga aplicada e o alongamento [1].
Com isso, é possível avaliar qual o limite de resistência a tração do material, quando o material continua seu processo de encruamento, mas também a ocorrência de falhas na estrutura com uma taxa maior apresenta a diminuição de sua resistência mecânica, ou seja, é mais “fácil” de deformar o material, é necessária uma menor tensão para tal.
Precisa de aços para ferramentas? Solicite sua cotação com a Serrametal! ⬇

Conteúdo não pode ser publicado ou redistribuído sem prévia autorização. Elaboração e Edição: Thiago Cortiz e Renata Brandolin
Referências
[1] Callister Jr., W. D. Fundamentos da ciência e engenharia de materiais. Rio de Janeiro: LTC Editora, 2006;
[2] John Newman, Phil Owens, 2 – Properties of lightweight concrete, Editor(s): John Newman, Ban Seng Choo, Advanced Concrete Technology, Butterworth-Heinemann, 2003, Pages 3-29, ISBN 9780750656863, https://doi.org/10.1016/B978-075065686-3/50288-3.
(http://www.sciencedirect.com/science/article/pii/B9780750656863502883)
[3] MARTIN, E.; LEGUILLON, D.; SEVECEK, O.; BERMEJO, R.. Understanding the tensile strength of ceramics in the presence of small critical flaws. Engineering Fracture Mechanics, [S.L.], v. 201, p. 167-175, out. 2018. Elsevier BV. http://dx.doi.org/10.1016/j.engfracmech.2018.06.021.
[4] Danzer R. A general strength distribution function for brittle materials. J Eur Ceram Soc 1992;10:461–72.
[5] Danzer R. On the relationship between ceramic strength and the requirements for mechanical design. J Eur Ceram Soc 2014;34:3435–60.
[6] Usami S, Kimoto H, Takahashi I, Shida S. Strength of ceramic materials containing small flaws. Eng Fract Mech 1986;23:745–61
[7] BRAGANCA, S. R.; BERGMANN, C. P.. Aspectos teóricos e práticos sobre a resistência mecânica de porcelanas. Cerâmica, São Paulo , v. 50, n. 314, p. 145-155, June 2004 . Available from <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0366-69132004000200012&lng=en&nrm=iso>. access on 27 Jan. 2021. https://doi.org/10.1590/S0366-69132004000200012.
[8] CANEVAROLO JR, S. V. Ciência dos Polímeros – Um texto básico para tecnólogos e engenheiros. 2ª edição., São Paulo: Artliber, 2002.
[9] BILLMEYER, F W.; Textbook of polymer science. 3. ed. New York, USA: Wiley, c1984, 578.
[10] SPERLING, L H.; Introduction to physical polymer science. 4. ed. New Jersey, USA: John Wiley & Sons, 2006, 845
[11] ASTM D638-14, Standard Test Method for Tensile Properties of Plastics, ASTM International, West Conshohocken, PA, 2014, www.astm.org
[12] ASTM D882-18, Standard Test Method for Tensile Properties of Thin Plastic Sheeting, ASTM International, West Conshohocken, PA, 2018, www.astm.org
[13] Askeland, D.R.; Phulé, P.P. Ciência e Engenharia dos Materiais. Cengage Learning. 2008. Cap. 8; Cap. 10, Seções 10-4; Cap. 11, Seção 11-1.
[14] MELLO, Alexandre Galvão Brasileiro de. Influência da deformação plástica na corrosão de aço carbono, aço inoxidável e cobre em sistemas de resfriamento
[15] MENDES FILHO, Anibal de Andrade. Microstructural evolution and properties of pure titanium grade 2 subjected to severe plastic deformation. 2015. 190 f. Tese (Doutorado em Ciências Exatas e da Terra) – Universidade Federal de São Carlos, São Carlos, 2015.
[16] N. Saba, M. Jawaid, M.T.H. Sultan, 1 – An overview of mechanical and physical testing of composite materials, Editor(s): Mohammad Jawaid, Mohamed Thariq, Naheed Saba, In Woodhead Publishing Series in Composites Science and Engineering, Mechanical and Physical Testing of Biocomposites, Fibre-Reinforced Composites and Hybrid Composites, Woodhead Publishing, 2019, Pages 1-12, ISBN 9780081022924, https://doi.org/10.1016/B978-0-08-102292-4.00001-1.
[17] Gross D, Hauger W, Schroder J, Wall W, Bonet J. Engineering Mechanics 2, Springer. 2011